Q&A
【電験三種Q&A(4)】「静電気に関するクーロンの法則」について

Question
真空中の直線上に間隔 r〔m〕を隔てて、点A、B、Cがあり、
各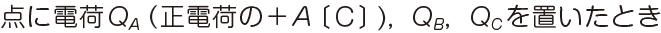 、これらの 3 つの点電荷に働く力がそれぞれ 0 になったという条件の問題で、解説に「点Bは負電荷、Cは正電荷となる」とあります。
、これらの 3 つの点電荷に働く力がそれぞれ 0 になったという条件の問題で、解説に「点Bは負電荷、Cは正電荷となる」とあります。

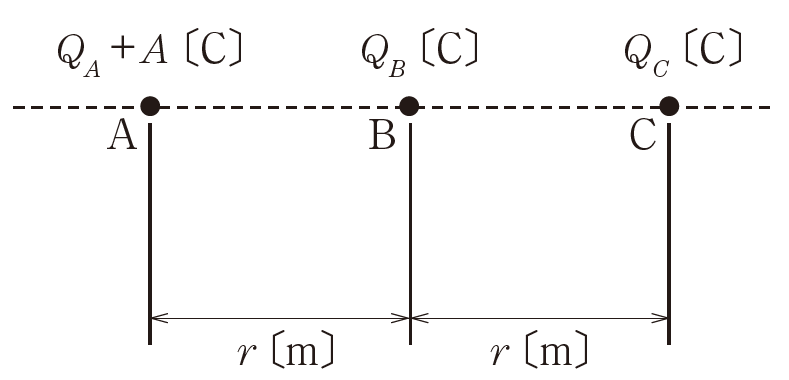
【図1】

【図1】
Answer
静電気に関するクーロンの法則により、2 つの電荷間の力は、同符号では反発、異符号では吸引します。
この問題では点電荷は 3 個ありますから、各点電荷に働くクーロン力は、自分を除く残り 2 つからの電荷によるクーロン力の合成となります。
ここから、次のように順番に考えていきましょう。
この問題では点電荷は 3 個ありますから、各点電荷に働くクーロン力は、自分を除く残り 2 つからの電荷によるクーロン力の合成となります。
ここから、次のように順番に考えていきましょう。
2 つの力の合成が 0 ということは、この 2 つのクーロン力は必ず力の方向が逆ということになります。
問題では、点Aだけが正電荷として値が与えられています。図1において点Bには、点Aと点Cからの 2 つの力が働きますから、力の合成が 0 になるためには、点Cの電荷による力の向きは、点Aとは逆になります。
すなわち、力の方向を考えると、
- ① 点Bに対し点Aの力
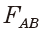 が吸引(左向き)なら、点Cからの力も吸引(右向き)
が吸引(左向き)なら、点Cからの力も吸引(右向き) - ② 点Bに対し点Aの力
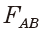 が反発(右向き)なら、点Cからの力も反発(左向き)
が反発(右向き)なら、点Cからの力も反発(左向き)
となることが必要ですから、
点Bに対して点Aと点Cは吸引か反発の同じ働きをしています。
したがって、点Aと点Cは同符号となり、点Cは正電荷と判断できます。
すると、点Cに対して点Aの力 ![]() は反発力になります。点Cの合成力を 0にするには、力
は反発力になります。点Cの合成力を 0にするには、力 ![]() の反発力を打ち消すため、点Bからの力は吸引力が必要です。
の反発力を打ち消すため、点Bからの力は吸引力が必要です。
すなわち点Bの符号は点Cとは逆になりますから、点Bは負電荷となります。
JTEX 電験三種対策講座ラインナップ


4科目を受講する「徹底マスターコース」「総合コース」のほか、科目別合格を目指す方のために「科目別コース」を設けています。
また、テーマ別に過去問題を厳選し、重要ポイントを絞ってわかりやすく解説した「科目別Web講義コース」も加わり、豊富なラインナップの中からご自身の勉強方法に合わせてコース選択が可能です。


 メニュー
メニュー 閉じる
閉じる


